You are here: Foswiki>Homepages Web>CreateHomepageTopic>HomepageMartinJurkovic>Meeting20070529MartinJurkovic (2007-06-14, MartinJurkovic)Edit Attach
Total scattering in RICH
Total scattering was calculated using the formula: Theta_0 = 13.6 MeV/(beta*c*p) * Z * sqrt(SUM) * {1 + 0.038 * ln(SUM)}where SUM = sum(x_i / X0_i)
Taking into account electrons, than beta = Z = 1
| Total scattering angle as a function of polar angle and momenta. |
|---|
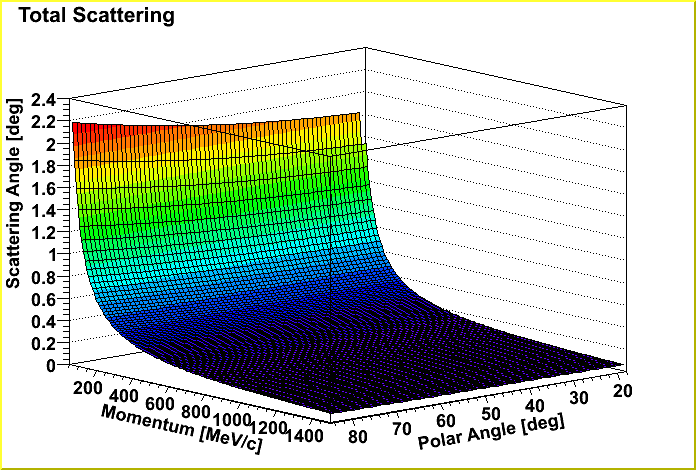 |
| Total scattering angle as a function of momenta for different polar angles. |
|---|
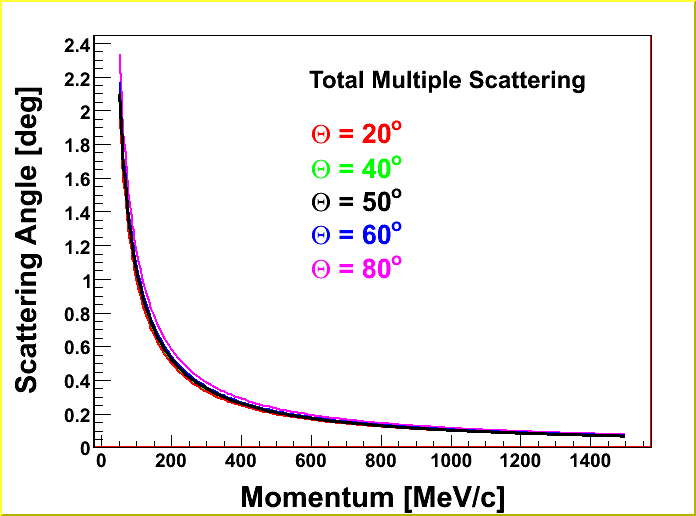 |
In the calculation, the polar angle dependant deflection between the perpendicular direction to the surface of the RICH components (shortest distance through the materials) and particle incident angle (real particle path length through the material) was taken into account.
| Dependance of the deflection angle on the polar angle. |
|---|
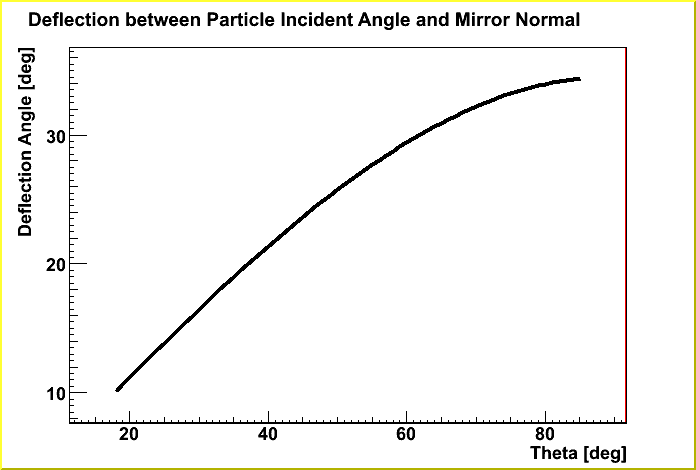 |
Small Angle Scattering divided in all RICH components
Scattering in the radiator gas C4F10
- Properties of C4F10
- Density: 24.61 g/cm**3 (at 20deg Celsius, 2.28bar, gas phase)
- Density: 1516 g/cm**3 (at 20deg Celsius, liquid phase)
- Radiation Length X0 = 34.52 g/cm**2 = 3200 cm in the gas phase at atmospheric pressure
| Small angle scattering in RICH radiator as a function of polar angle and momenta. |
|---|
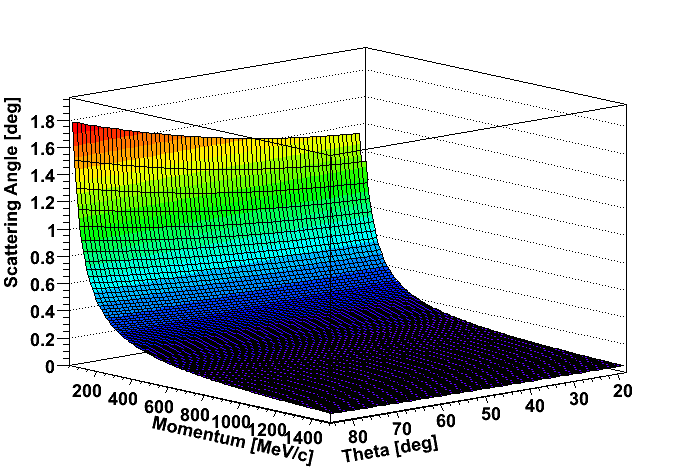 |
| Dependance of the particle trajectory length in the RICH radiator on the polar angle. |
|---|
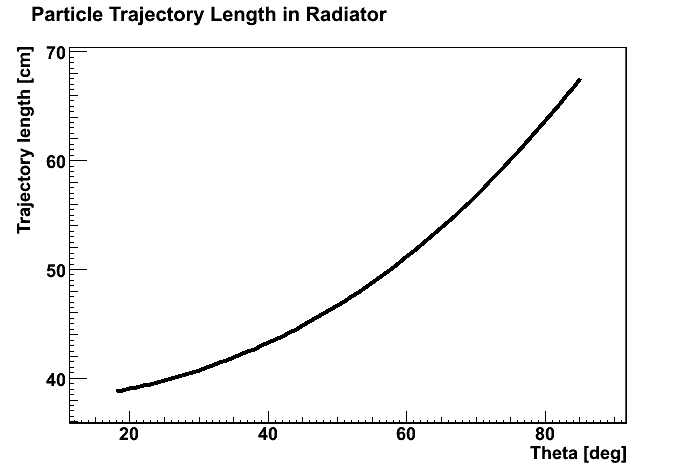 |
| Scattering angle in RICH radiator as a function of momenta for different polar angles. | Scattering angle in RICH radiator as a function of momenta for polar angle Theta = 50deg. |
|---|---|
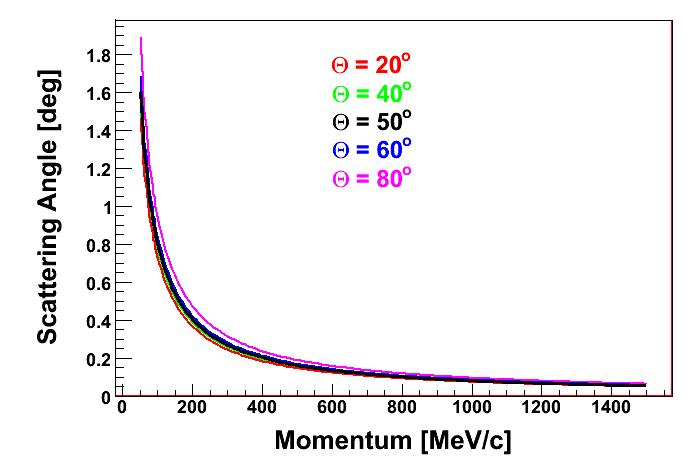 |
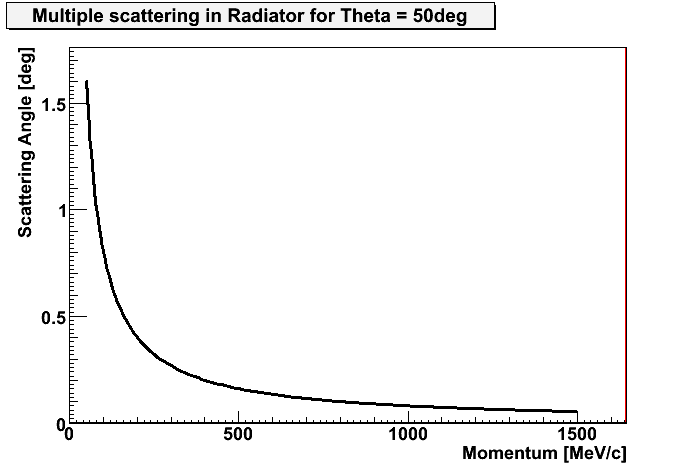 |
In the following, only the mean deflection to the perpendicular direction of 22.25deg was taken into account to make the pictures simple
Scattering in SIGRADUR (mirror substrate material)
- Properties of SIGRADUR
- Mean thickness = 2.1 mm
- Radiation length X0 = 28 cm
| Scattering angle in RICH mirror substrate material SIGRADUR as a function of momenta for mean deflection angle 22.25deg |
|---|
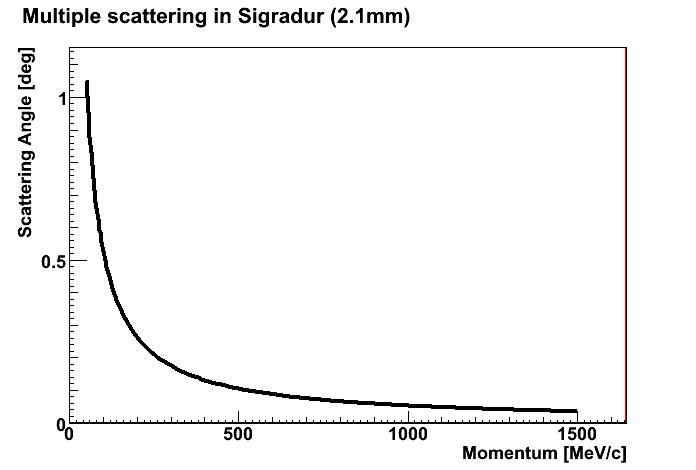 |
Scattering in the mirror reflective and protection layer
- Properties of Aluminum (reflective layer)
- Thickness = 20 ug/cm**2
- Density = 2.7 g/cm**3
- Radiation length X0 = 24.01 g/cm**2 = 8.9 cm
- Properties of MgF2 (protection layer)
- Thickness = 11 ug/cm**2
- Density = 3.0 g/cm**3
- Radiation length X0 = 29.32 g/cm**2 = 9.77 cm
| Scattering in Aluminium. | Scattering in MgF2. |
|---|---|
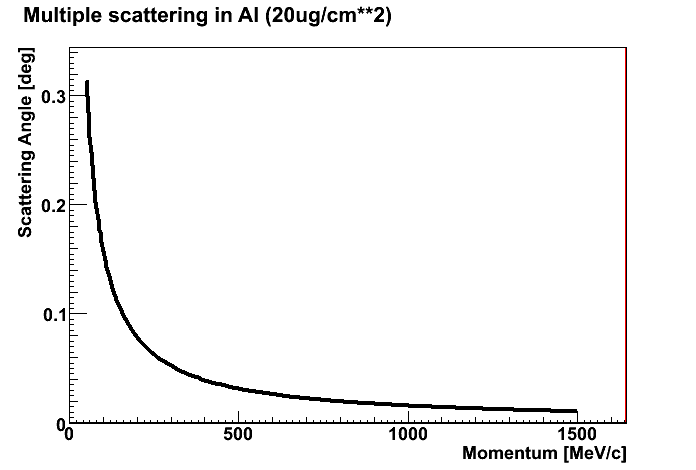 |
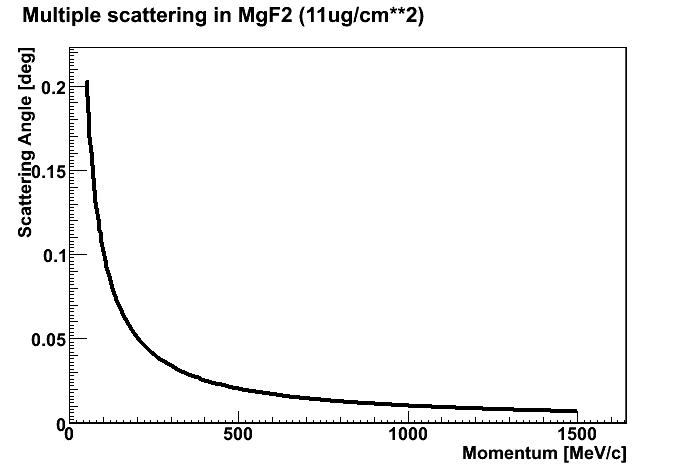 |
Scattering in the carbon shell (CFK)
- Properties of CFK
- Thickness = 0.4 mm
- Radiation length X0 = 28 cm
| Scattering in CFK |
|---|
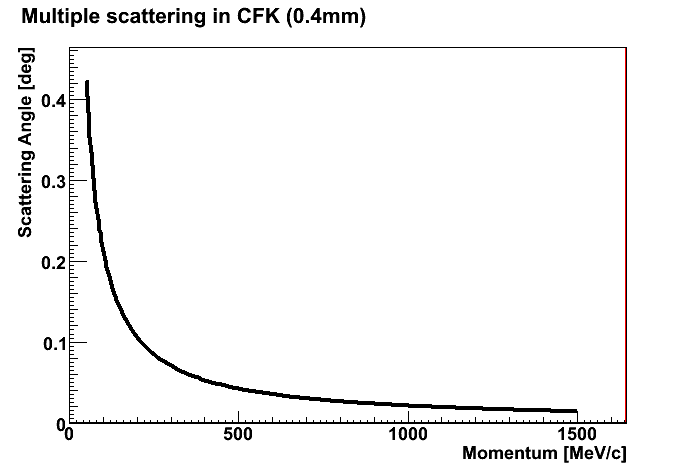 |
Elliptic (circular) vs rectangular matching cut
Area difference between these two cuts is:- Rectangular cut: (2*D_phi)*(2*D_theta) = 4*D_theta*D_phi
- Elliptic cut: pi * D_theta * D_phi
- Difference = (4 - pi)/4 = 22%
Conversion / Signal from PLUTO simulation
I have compared the 1D distribution for (theta_rich - theta_RK) (in phi it looks similar) for electrons coming from conversion and the electrons coming from all other sources. the conversion signal I have chosen according to the following condition: "pid.genInfo1==7001 || pid.genInfo1==17001 || pid.genInfo1==52001", the "real" signal is negation of the previous condition. the determination of the mean and sigma of the distribution was done with the "standard" 2-gaussian fit for momentum bins (0,150>; (150,350> and (350,1000> in the picture "compareSim.png" you can see mean and sigma of the delta_theta distributions for the 3 momenta bins. the upper two pictures are done for electrons and positrons separately (red color "real" signal, blue conversion signal). in the lowest picture the comparision between electrons and positrons for the "real" signal is done. as one can see, the differences in the simulation are only minor. the yields for signal and conversion are comparable (almost 1:1) for momenta (0,150>, it drops to 2:1 for momenta (350,1000> (see thetaNeg.jpg) The sigma of the delta_theta distributions for negative tracks is:- Signal: 0.96, 0.74, 0.54
- Conversion: 1.01, 0.81, 0.62
- Signal: 1.18, 0.79, 0.60
- Conversion: 1.12, 0.88, 0.60
==================================================
in phi are the distributions much more narrower:
The sigma of the delta_phi distributions for negative tracks is: - Signal: 0.55, 0.47, 0.47
- Conversion: 0.40, 0.53, 0.56
- Signal: 0.57, 0.49, 0.50
- Conversion: 0.46, 0.51, 0.40
- Comparision delta theta (RICH - MDC) distribution of signal and conversion leptons:
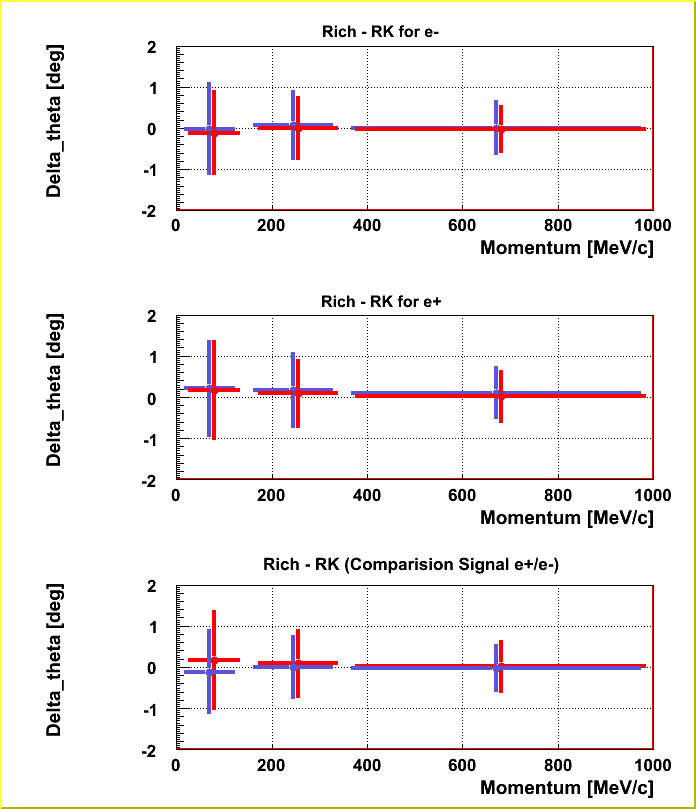
- Phi correlation for positive leptons (signal left, conversion right):
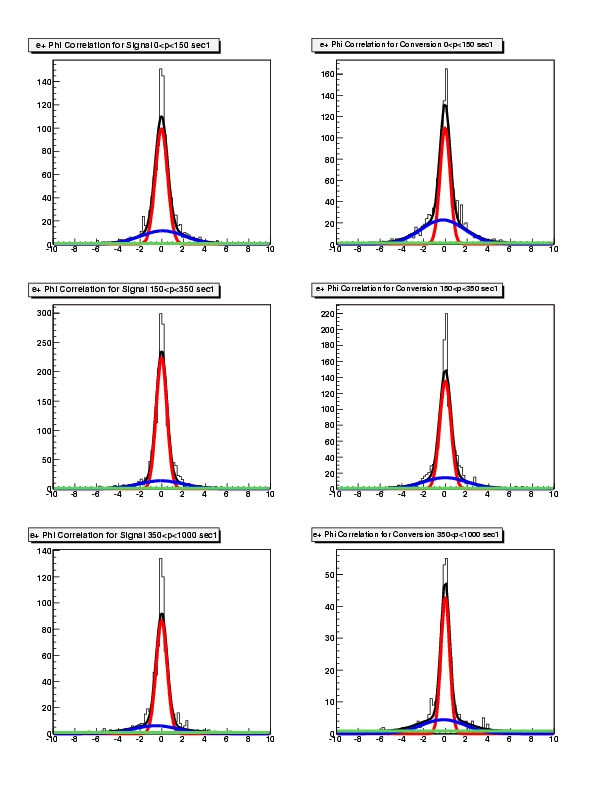
- Theta correlation for positive leptons (signal left, conversion right):
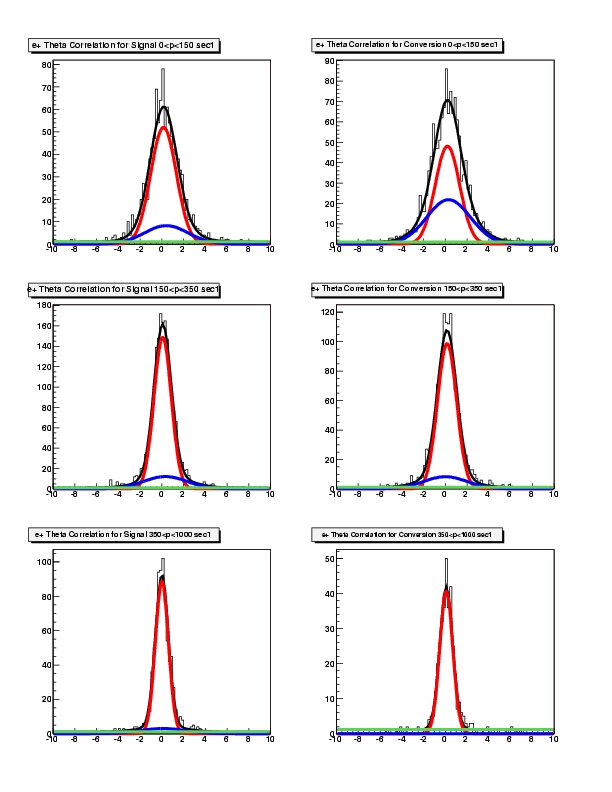
-- MartinJurkovic - 29 May 2007
| I | Attachment | Action | Size | Date | Who | Comment |
|---|---|---|---|---|---|---|
| |
scattering50.txt | manage | 3 K | 2007-06-12 - 14:32 | MartinJurkovic | Total scattering and scattering in radiator as a function of momenta at polar angle 50deg |
| |
theta2length.txt | manage | 1 K | 2007-06-12 - 14:31 | MartinJurkovic | Path length and deflection angle as a function of polar angle |
Edit | Attach | Print version | History: r7 < r6 < r5 < r4 | Backlinks | View wiki text | Edit wiki text | More topic actions
Topic revision: r7 - 2007-06-14, MartinJurkovic
Copyright © by the contributing authors. All material on this collaboration platform is the property of the contributing authors.
Ideas, requests, problems regarding Foswiki Send feedback | Imprint | Privacy Policy (in German)
Ideas, requests, problems regarding Foswiki Send feedback | Imprint | Privacy Policy (in German)


